L'area di un triangolo qualsiasi
In base ai teoremi enunciati sui triangoli rettangoli si può facilmente ottenere una formula per il calcolo dell'area di un triangolo qualsiasi in funzione di due lati e dell'angolo tra essi compreso.
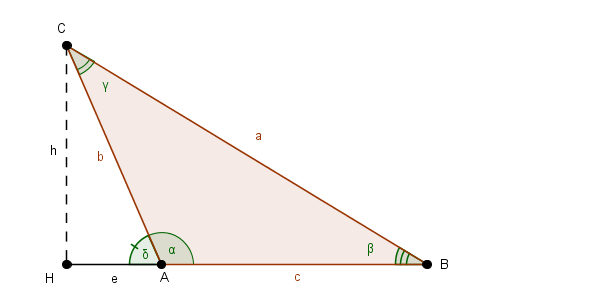
Infatti riferendosi alla figura seguente si può vedere che l'altezza del triangolo 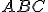 relativa al lato
relativa al lato 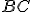 è data da
è data da
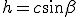 .
.
dunque per l'area si ha
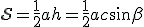 ,
,
pertanto
Teorema
In un triangolo qualsiasi l'area della superficie è pari al semiprodotto tra due suoi lati ed il seno dell'angolo compreso tra essi.
Si sottolinea ancora una volta che il triangolo 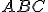 non è necessariamente rettangolo.
non è necessariamente rettangolo.
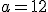 e
e  , e l'angolo tra essi compreso è tale che
, e l'angolo tra essi compreso è tale che 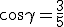 .
.
Nella dimostrazione sopra riportata per il calcolo dell'area si è preso in considerazione un triangolo acutangolo, ma è facile estendere la dimostrazione anhe al caso in cui l'angolo compreso tra i due lati è ottuso, infatti, con riferimento alla figura sottostante, gli angoli 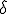 e
e 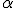 sono supplementari, dunque hanno lo stesso seno. Pertanto
sono supplementari, dunque hanno lo stesso seno. Pertanto
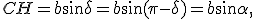 dunque ancora una volta
dunque ancora una volta
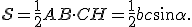
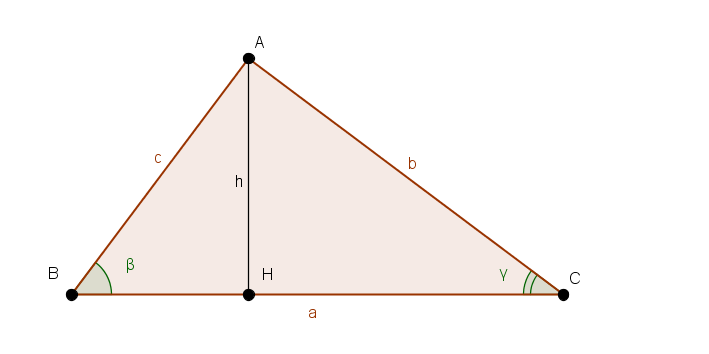
Ovviamente il teorema può essere usato anche in senso inverso. Ad esempio si voglia determinare l'angolo compreso tra due lati  e
e 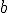 di un triangolo sapendo che le misure dei lati sono rispetivamente
di un triangolo sapendo che le misure dei lati sono rispetivamente 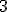 e
e 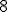 e che l'area del triangolo misura
e che l'area del triangolo misura 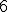 .
.
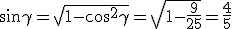 ,
,
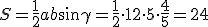 .
.
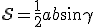 si ricava la formula inversa:
si ricava la formula inversa: 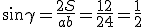 .
.
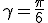 .
.