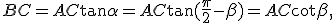I teoremi sui triangoli rettangoli
In questa sezione verranno introdotti i teoremi sui triangoli rettangoli ed in seguito si vedranno alcuni esempi per la loro applicazione.
Dato un triangolo rettangolo  lo si immagini immerso in un sistema di riferimento cartesiano, in modo che uno dei cateti si sovrapponga al semiasse positivo delle ascisse e l'ipotenusa abbia un vertice nell'origine.
lo si immagini immerso in un sistema di riferimento cartesiano, in modo che uno dei cateti si sovrapponga al semiasse positivo delle ascisse e l'ipotenusa abbia un vertice nell'origine.
Nello stesso riferimento si consideri, poi, la circonferenza trigonometrica, ossia la circonferenza di centro l'origine degli assi e raggio unitario, e si denotino con D ed E rispettivamente l'intersezione dell'ipotenusa con la circonferenza e la sua proiezione sull'asse delle ascisse.
Le suddette uguaglianze si riassumono nel seguente:
Teorema
In un triangolo rettangolo un cateto è uguale all'ipotenusa per il coseno dell'angolo compreso tra l'ipotenusa ed il cateto, ed è uguale all'ipotenusa per il seno dell'angolo opposto al cateto.
 l'angolo
l'angolo 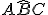 , allora dal precedente teorema dovrebbe risultare
, allora dal precedente teorema dovrebbe risultare 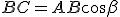 , ma è anche
, ma è anche 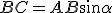 , come mai?
, come mai?
In base al teorema precedente si deduce subito che vale anche il seguente :
Teorema
In un triangolo rettangolo un cateto è uguale al prodotto dell'altro cateto per la tangente dell'angolo opposto oppure al prodotto dell'altro cateto per la cotangente dell'angolo acuto adiacente al primo cateto.
Basterà, infatti, dividere membro a membro le uguaglianze
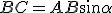 e
e 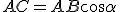
per ottenere:
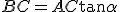 ,
,
oppure
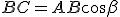 e
e 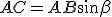 per avere:
per avere:
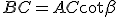 ,
,
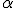 e
e 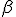 di un triangolo rettangolo si ha
di un triangolo rettangolo si ha 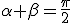 .
.
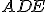 sono simili, quindi si ottengono le seguenti uguaglianze:
sono simili, quindi si ottengono le seguenti uguaglianze:
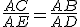 e
e 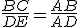 ,
,
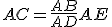 e
e 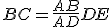 .
.
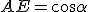 ,
, 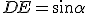 e
e 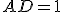 ,
,
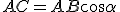 e
e 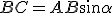
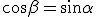 .
.