Il teorema delle proiezioni
Grazie ai teoremi visti sul triangolo rettangolo è possibile dedurre un teorema che permette di esprimere uno dei lati di un triangolo qualsiasi in funzione degli altri due lati e degli angoli adiacenti al primo lato.
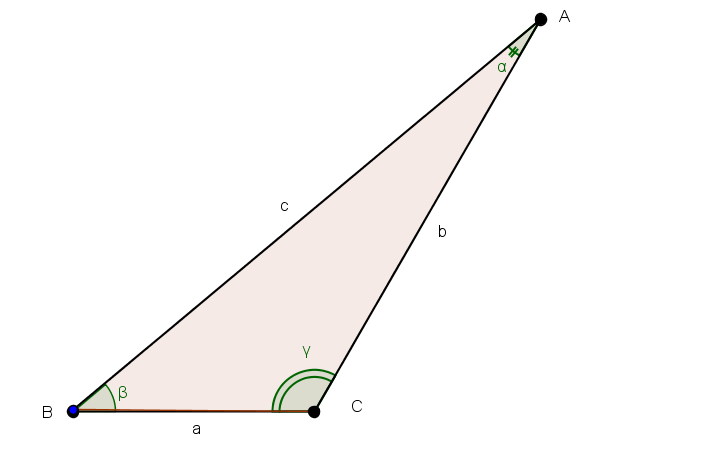
Per la simbologia si fa riferimento alla figura che segue.
Teorema delle proiezioni.
Il lato 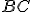 di un triangolo qualsiasi
di un triangolo qualsiasi 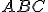 è pari alla somma dei prodotti tra ciascuno degli altri due lati ed il coseno dei rispettivi angoli compresi con il lato incognito. Precisamente:
è pari alla somma dei prodotti tra ciascuno degli altri due lati ed il coseno dei rispettivi angoli compresi con il lato incognito. Precisamente:
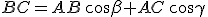 .
.
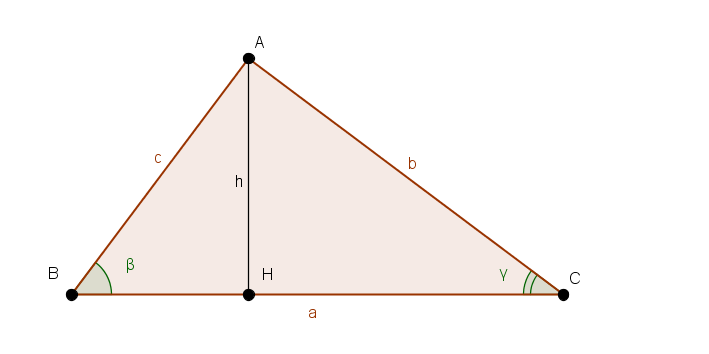
La tesi del teorema si ottiene osservando che, con riferimento alla figura, il lato 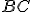 è la somma
è la somma
delle proiezioni su di esso dei lati 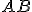 e
e 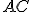 . Poichè i triangoli
. Poichè i triangoli 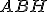 e
e 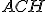 sono per costruzione rettangoli,
sono per costruzione rettangoli,
dai precedenti teoremi ciascuna proiezione si ottiene moltiplicando un lato per il coseno dell'angolo
che forma con 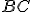 , da cui segue la tesi.
, da cui segue la tesi.
Dato un triangolo 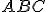 di esso si conoscono le misure di due lati, b=23 e c=31, e gli angoli
di esso si conoscono le misure di due lati, b=23 e c=31, e gli angoli
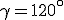 e
e 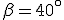 . Si calcoli il perimetro del triangolo ( si vede la figura di seguito ).
. Si calcoli il perimetro del triangolo ( si vede la figura di seguito ).
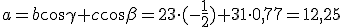 .
.
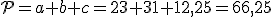 .
.