Il teorema della corda
Si supponga di avere una circonferenza di raggio  e centro
e centro 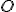 , e sia
, e sia 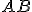 una sua qualsiasi corda. Sia
una sua qualsiasi corda. Sia 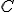 un qualsiasi altro punto della circonferenza su uno degli archi individuati da
un qualsiasi altro punto della circonferenza su uno degli archi individuati da 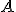 e
e 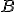 , si dice che l'angolo
, si dice che l'angolo 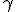 è un angolo alla circonferenza che sottende la corda
è un angolo alla circonferenza che sottende la corda 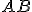 .
.
Dalla geometria euclidea si sa che l'ampiezza dell'angolo 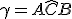 non dipende dal punto
non dipende dal punto 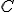 , ma solo dalla lunghezza della corda fissata
, ma solo dalla lunghezza della corda fissata 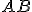 . Inoltre se
. Inoltre se 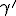 è l'angolo alla circonferenza che sottende sempre la corda
è l'angolo alla circonferenza che sottende sempre la corda 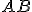 , ma con vertice sull'altro arco individuato dalla stessa corda, allora
, ma con vertice sull'altro arco individuato dalla stessa corda, allora 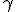 e
e 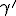 sono tra loro supplementari.
sono tra loro supplementari.
Di seguito viene riportata una figura sulla quale lo studente può liberamente muovere alcuni elementi. Grazie ad essa, seguendo anche le indicazioni proposte nelle "riflessioni" che seguono, si è invitati a verificare praticamente alcune proprietà geometriche.
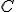 sulla circonferenza, cosa osservi?
sulla circonferenza, cosa osservi?
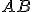 , cosa osservi sull'angolo
, cosa osservi sull'angolo 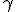 ?
?
Cerca di fare in modo che la corda 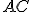 sia un diametro della circonferenza, cosa osservi sull'angolo
sia un diametro della circonferenza, cosa osservi sull'angolo 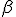 ?
?
Da quest'ultima osservazione, tenendo conto della risoluzione dei triangoli rettangoli, ed osservando che nella sottostante figura l'angolo 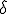 è uguale all'angolo
è uguale all'angolo 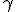 perché sottendono la stessa corda, si può subito dedurre il seguente:
perché sottendono la stessa corda, si può subito dedurre il seguente:
Teorema [ della corda ].
Detto 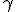 l'angolo che sottende una corda
l'angolo che sottende una corda 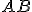 in una circonferenza di raggio
in una circonferenza di raggio  , vale la seguente uguaglianza:
, vale la seguente uguaglianza:
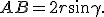
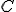 passa da un arco ad un altro. Lungo lo stesso arco l'ampiezza dell'angolo resta costante.
passa da un arco ad un altro. Lungo lo stesso arco l'ampiezza dell'angolo resta costante.