Soluzioni esercizio 5
Nota che la funzione non è definita per x=0.
Osserva anche che per valori di x sempre più grandi e per valori di x sempre più piccoli la funzione si avvicina all'asse x senza mai toccarlo; si dice che la funzione è asintotica all' asse x.
Osserva ancora che per valori di x molto prossimi allo zero, la funzione assume valori sempre più grandi se ci avviciniamo a zero da destra, e valori sempre più piccoli se ci avviciniamo a zero da sinistra; si dice che la funzione è asintotica all' asse y.
) Funzione traslata verticalmente verso l'alto di 1 unità:
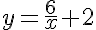
y=f(x)+2
nel nostro caso diventa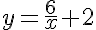
rappresentata in verde qui di seguito.
Osserva che per x=0 la funzione non è definita, esattamente come succedeva prima della traslazione verticale.
Si può anche osservare che prima della traslazione la funzione era asintotica all'asse x (cioè si avvicinava sempre più all'asse x senza mai toccarlo): dopo la traslazione verticale effettuata ora la funzione è asintotica alla retta y=2.
b) Funzione traslata orizzontalmente verso sinistra di 3 unità:
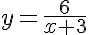
y=f(x+3)
nel nostro caso diventa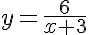
rappresentata in blu qui di seguito.
Osserva che la funzione traslata risulta definita per x=0 ma non più per x=-3. Con la traslazione orizzontale si sposta l'asintoto verticale che non è più l'asse y ma le retta di equazione x=-3.
c) Funzione traslata orizzontalmente verso destra di 3 unità e verso l'alto di 4 unità:
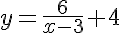 rappresentata in viola qui di seguito.
rappresentata in viola qui di seguito.
Osserva che con la traslazione obliqua si modificano sia l'asintoto orizzontale che quello verticale.
y=f(x-3)+4
nel nostro caso diventa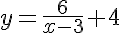
Osserva che con la traslazione obliqua si modificano sia l'asintoto orizzontale che quello verticale.