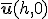Muovi il punto C
Negli assi cartesani qui sotto sono rappresentati due punti: C e D e le loro coordinate.
Il punto C è libero di muoversi ovunque nel piano, mentre il punto D è vincolato in qualche modo a C.
Vogliamo determinare in che modo C è vincolato a D.
Muovi il punto C nei vari quadranti e confronta i valori assunti dalle coordinate dei due punti.
Che cosa puoi osservare?
1) Comunque si muova il punto C, il punto D mantiena la stessa ascissa (x) del punto C
Vero Falso
2) Comunque si muova il punto C, il punto D mantiena la stessa ordinata (y) del punto C
Vero Falso
3) Le ascisse dei due punti sono sempre diverse tra di loro, ma quella di D è, in ogni situazione, maggiore di quella di C
Vero Falso
4) Possiamo dire che xD=xC+2 anche quando le ascisse sono negative cioè siamo nel II o III quadrante
Vero Falso
5) Se le coordinate del primo punto sono C(x,y) allora le coordinate del secondo punto sono D(x+2,y+2)
Vero Falso
6) Se vogliamo che il punto D stia a sinistra del punto C di tre unità dovremo avere che xD=xC-3
Vero Falso
|
Possiamo dire che il punto D si ottiene con una traslazione orizzontale del punto C. Le coordinate dei due punti sono strettamente vincolate: C(x,y) diventa nella traslazione orizzontale D(x+h,y) dove h rappresenta di quanto si incrementa (se positivo) o decrementa (se negativo) il valore dell'ascissa di C.
Si dice anche che il punto D si ottiene dal punto C con una traslazione di vettore
|