La scrittura degli archi
Con il simbolo Z si indicano i numeri interi cioè l'insieme dei numeri
........ -4, -3, -2, -1, 0, +1, +2, +3, +4, .......
La misura di tutti gli infiniti archi AB rappresentabili con la figura
può essere scritto nel seguente modo:
|
|
Il punto B infatti, può aver raggiunto la posizione indicata, dopo aver descritto in verso antiorario
| un quarto di circonferenza | in questo caso k=0 | l'arco è AB = 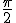 r r |
| un giro completo più un quarto di circonferenza | in questo caso k=1 | l'arco è AB = 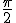 r+2 r+2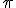 r r |
| due giri comleti più un quarto di circonferenza | in questo caso k=2 | l'arco è AB = 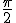 r+4 r+4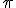 r r |
| tre giri comleti più un quarto di circonferenza | in questo caso k=3 | l'arco è AB = 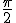 r+6 r+6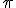 r r |
| etc... |
ma il punto B può aver ragginto la posizione indicata anche dopo aver descritto in verso orario
| tre quarti di circonferena | in questo caso k=-1 | l'arco AB =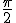 r-2 r-2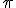 r= -3 r= -3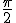 r r |
| un giro completo più tre quarti di circonferenza | in questo caso k=-2 | l'arco AB = =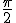 r-4 r-4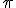 r= -7 r= -7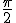 r r |
| etc... |
|
Una stessa figura individua infiniti archi; si sceglie come
"RAPPRESENTANTE" (o PRINCIPALE)
quello positivo minore della circonferenza. Così, nell'esempio precedente, l'arco principale è
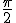 r
r
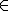 Z
Z