LA CIRCONFERENZA GONIOMETRICA
Lo studio delle funzioni goniometriche sen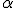 , cos
, cos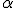 e tg
e tg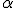 si possono studiare mediante l'introduzione della circonferenza goniometrica.
si possono studiare mediante l'introduzione della circonferenza goniometrica.
Preso un angolo 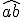 di misura
di misura 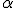 , costruiamo un sistema di riferimento cartesiano centrato nel vertice O dell'angolo e con semiasse positivo delle ascisse coincidente con la semiretta a. Consideriamo come unità di misura la lunghezza del segmento OP.
, costruiamo un sistema di riferimento cartesiano centrato nel vertice O dell'angolo e con semiasse positivo delle ascisse coincidente con la semiretta a. Consideriamo come unità di misura la lunghezza del segmento OP.
In questo sistema di riferimento la circonferenza ha equazione
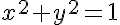
e viene detta circonferenza goniometrica.
Avendo posto OP=1 si ha, più semplicemente,
sen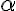 =HP =HP |
cos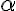 =OH =OH |
In questo modo, seno e coseno risultano essere, rispettivamente, l'ordinata e l'ascissa del punto P.
Consideriamo poi la retta di equazione x=1 e chiamiamo T il punto in cui interseca la semiretta b (o il suo prolungamento) e R il punto di coordinate (1;0).
Otteniamo che
tg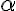 = =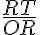 =RT =RT |
per cui la tangente risulta essere l'ordinata del punto che si trova sulla semiretta b (o sul suo prolungamento) avente acsissa 1.