Studio dei casi per la risoluzione di un triangolo
In questo paragrafo mediante alcuni esempi si analizzarenno i vari casi in cui è possibile risolvere un triangolo, ossia in base ai dati noti si può determinare ogni elemento del triangolo. Ovviamente il teorema da utilizzare dipenderà dai dati noti. Ad esempio non è possibile applicare il teorema dei seni se non si conosce alcun angolo che si oppone a qualche lato noto ( si vedano i casi 3. e 5. ).
I casi possibili sono i seguenti:
- sono noti due angoli ed il lato tra essi compreso;
- sono noti due angoli ed un lato non compreso tra essi;
- sono noti due lati e l'angolo tra essi compreso;
- sono noti due lati ed un angolo non compreso tra essi;
- sono noti i tre lati.
Chiaramente conoscere i tre angoli non è sufficiente, poiché in tal caso resta individuata un intera classe di triangoli simili.
Sono noti due angoli ed il lato tra essi compreso.
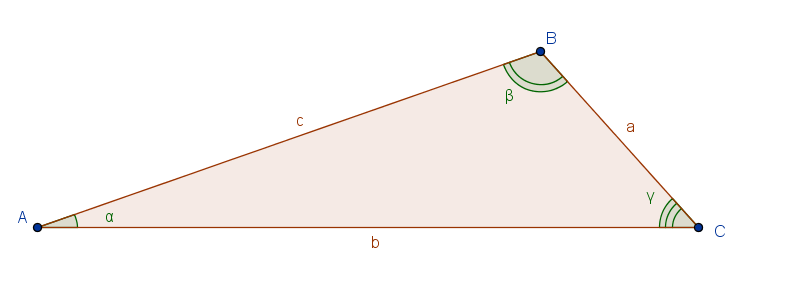
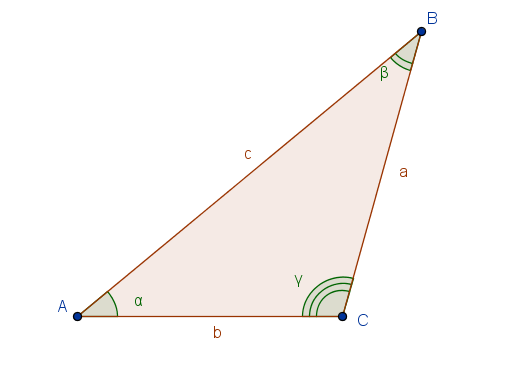
Del triangolo in figura sono noti il lato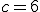 
e gli angoli 
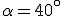e 
.
Sono noti due angoli ed un lato non compreso tra i due angoli.
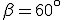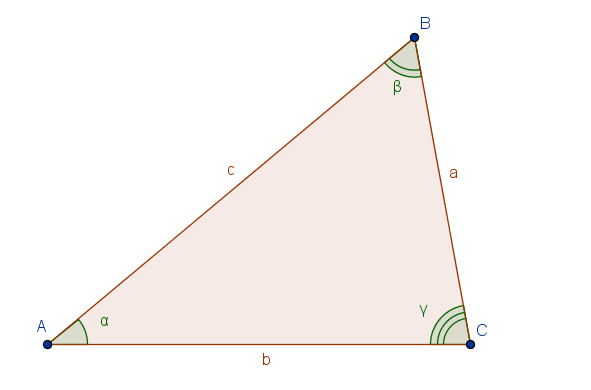
In questo caso uno degli angoli noti si oppone al lato dato, dunque si può applicare subito il teorema dei seni per calcolre un secondo lato. Infine per differenza si determina il terzo angolo e, sempre con il teorema dei seni il terzo lato.
E' evidente che il problema risulta essenzialmente identico al caso precedente, pertanto non si ritiene opportuno riportare un esempio numerico.
Sono noti due lati e l'angolo tra essi compreso.
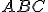di cui sono noti i lati 
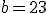e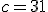 
e l'angolo 
.
,
.
.
Sono noti due lati ed un angolo non compreso tra i due lati.
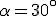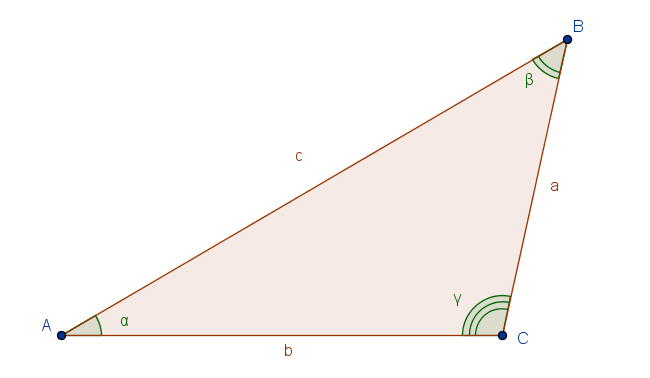
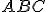di cui si conoscono i lati 
, 
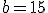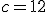e l'angolo 
.
,
.
,
.
Sono noti i tre lati.
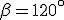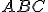del quale si conoscono le misure dei tre lati: 
, 
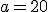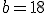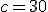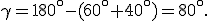
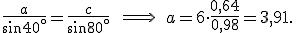
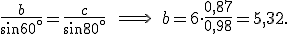
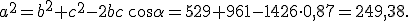
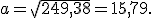
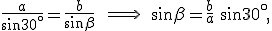
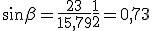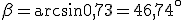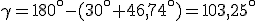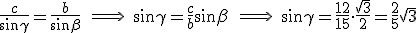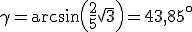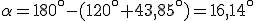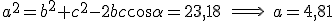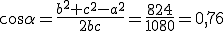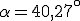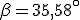e 
.
,
.
e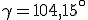 
.