Raggio del cerchio inscritto.

Si consideri un triangolo qualsiasi e sia il raggio del cerchio inscritto in esso.

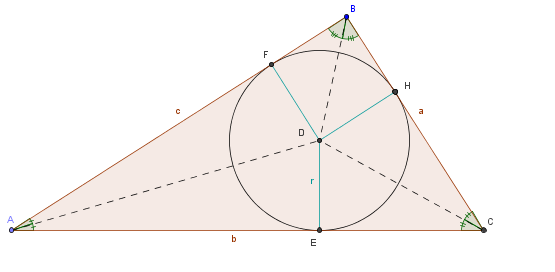
Detto 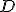il centro del cerchio ed 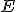, 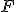e 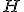i punti in cui esso è tangente ai lati del triangolo, i raggi ,

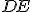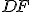
e 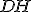sono perpendicolari ai rispettivi lati del triangolo. Quindi l'area 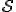del triangolo 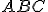si può esprimere

come somma delle aree dei triangoli 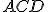, 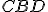e :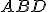

;

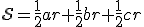dunque, esprimendo il raggio in funzione delle altre grandezze:

,

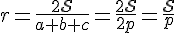
avendo indicato con 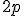il perimetro del triangolo. Pertanto vale il seguente:

Teorema.

In un triangolo il raggio del cerchio inscritto è pari al rapporto tra l'area del triangolo ed il suo semiperimetro.

Problema svolto

E' dato un triangolo rettangolo 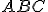con ipotenusa 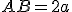e dell'angolo acuto 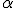si sa che 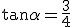.Si calcoli il raggio del cerchio inscritto al triangolo.

Sapendo che 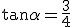, si può determinare il valore delle funzioni seno e coseno dello stesso angolo, infatti dalle identità :

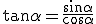, e 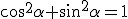segue:

,

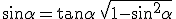elevando ambo i membri al quadrato e risolvendo rispetto a 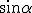si ottiene:

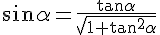
dove nell'estrazione della radice si è anche tenuto conto che l'angolo 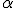è minore di .

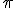Ora

,

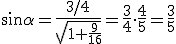poi, sempre dalla prima identità fondamentale, tenendo conto che :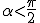

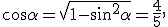
A questo punto si può risolvere il triangolo:

,

.

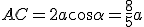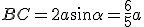Infine per calcolare il raggio del cerchio inscritto si calcola prima l'area ed il perimetro, e poi si applica la formula introdotta sopra:

,

,

Una formula per la mediana.

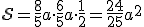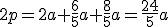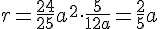
E' dato un triangolo 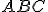di cui si conoscono le misure dei tre lati. Determinare la misura della mediana relativa al lato .

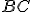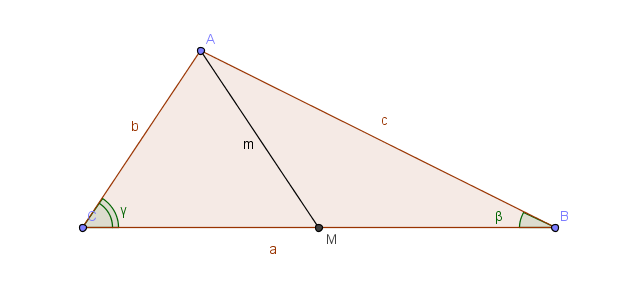
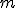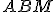Detta la mediana relativa al lato , si applica il teorema di Carnot ai triangoli e :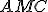

,

,

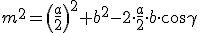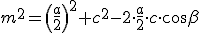sommando membro a membro

,

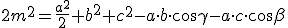raccogliendo negli ultimi due termini ed applicando il teorema delle proiezioni:

,

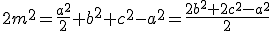infine ricavando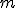

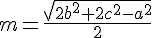
Pertanto si ottiene una formula che permette di calcolare la lunghezza di una mediana in funzione dei lati del triangolo.

Problema svolto.

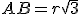In una circonferenza di raggio è data la corda , si conduca nel maggiore dei segmenti di cerchio determinati da 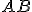, la corda 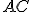che formi con 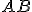l'angolo 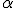. Determinare 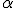in modo tale che si abbia:

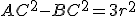
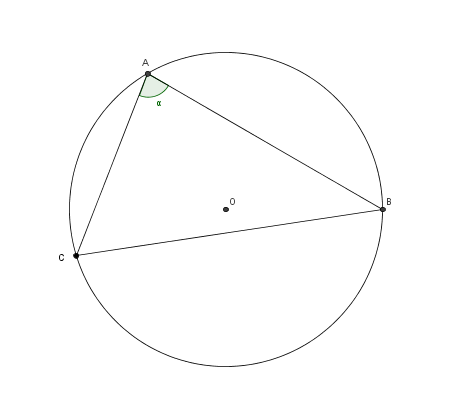
In questo tipo di problemi talvolta bisogna scegliere un angolo da assumere come incognita, però nel caso specifico è lo stesso testo ad indicarci qual è l'angolo incognito, quindi di seguito si pone, per comodità, 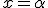. Inoltre è molto importante riconosce eventuali limiti geometrici per l'incognita scelta.

Intanto si osserva che, essendo 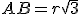, per il teorema della corda si ha 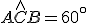. Allora l'angolo 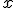, essendo interno al triangolo 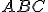, deve verificare le seguenti condizioni:

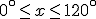
Dunque, per differenza, 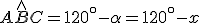. Pertanto

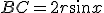e

.

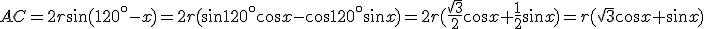Ora non resta che sostituire le espressioni trovate in funzione di 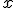nella formula del testo:

,

,

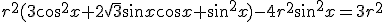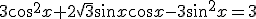riducendola ad omogenea e sommando i termini simili:

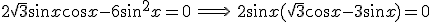, da cui , tenendo anche conto dei limiti geometrici imposti dal problema, si ottengono le soluzioni

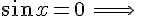
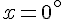
e

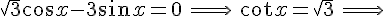
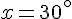
Si osservi che una delle possibili soluzioni rende il triangolo degenere, ma è comunque una situazione accettabile per la risoluzione del problema.