Ricordando il teorema di derivazione delle funzioni composte:

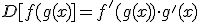
si ottiene, leggendo al "contrario" la formula, uno schema di integrazione che raggruppa svariate situazioni:

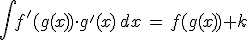
Ciascuno degli integrali della tabella precedente (Tabella 1) può quindi essere riletto come segue:

Tabella 2

1)		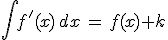2)
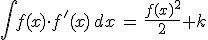3)		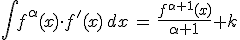4)
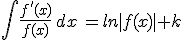5)		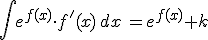6)
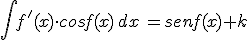7)		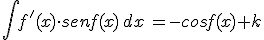8)
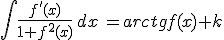9)		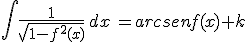10)
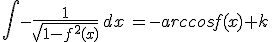11)		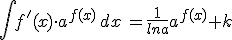12)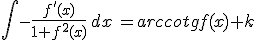