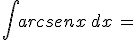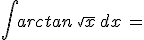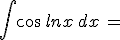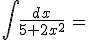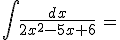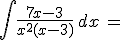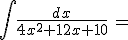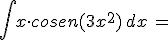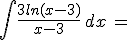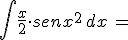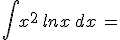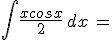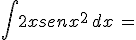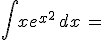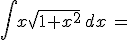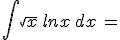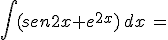Prova sommativa
Leggi il paragrafo seguente e completa le parti mancanti
Integrale indefinito
Il problema inverso a quello della derivazione consiste nella ricerca di tutte le funzioni la cui
sia uguale a una funzione assegnata. Questo problema è noto come ricerca delle
di una funzione. La totalità delle primitive di una funzione f(x) si chiama
della funzione f(x) e si indica con il simbolo: 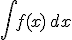 , che si legge "integrale indefinito della funzione f(x) in dx"; f(x) è detta funzione
.
, che si legge "integrale indefinito della funzione f(x) in dx"; f(x) è detta funzione
.
L'integrazione è quindi il processo
alla derivazione.
Ogni funzione continua in un intervallo ammette sempre integrale indefinito, ma non è detto che sia derivabile in ogni suo punto.
Sia f una funzione continua in un intervallo [a,b]: l'insieme di tutte le primitive di f in [a,b] si chiama integrale indefinito di f e si indica
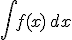
mentre la forma funzionale generica (in cui la costante è indefinita) di tale funzione è detta integrale indefinito di 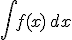 e si indica con
e si indica con
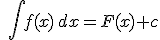
dove c rappresenta la
indefinita.
Metodi di integrazione
Per calcolare un integrale si può cercare di riconoscere nella funzione integranda la
di una qualche funzione (questi sono detti "integrali
").
Altrimenti esistono dei metodi che hanno come scopo la semplificazione della funzione integranda:
- se l'integranda è il prodotto di due funzioni, allora l'integrazione riduce l'integrale dato ad un altro integrale; se si è in grado di risolvere quest'ultimo si giunge al risultato richiesto.
- se il risultato non è immediatamente riconoscibile, è possibile effettuare un cambiamento di (integrazione per ) e ricondurre l'integrale dato ad un'altro nella nuova variabile
- se l'integranda è una funzione razionale fratta con denominatore di secondo grado si segue sempre lo stesso procedimento e precisamente:
- se il Δ del denominatore è
di zero ci si riconduce, attraverso il
di
dei polinomi, all'integrazione di due fratti
del tipo
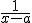 che porta alla primitiva
+ c
che porta alla primitiva
+ c - se il Δ del denominatore è
a zero ci si riconduce, attraverso il
di
dei polinomi, all'integrazione del fratto semplice
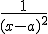 che porta alla primitiva
+ c
che porta alla primitiva
+ c - se il Δ del denominatore è
di zero ci si riconduce all'integrazione del fratto semplice
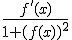 che porta alla primitiva
+ c
che porta alla primitiva
+ c
- se il Δ del denominatore è
di zero ci si riconduce, attraverso il
di
dei polinomi, all'integrazione di due fratti
del tipo
Principali primitive
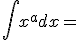 |
+ c |
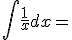 |
+ c |
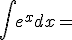 |
+ c |
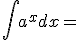 |
+ c |
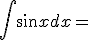 |
+ c |
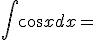 |
+ c |
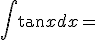 |
+ c |
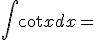 |
+ c |
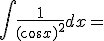 |
+ c |
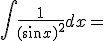 |
+ c |
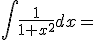 |
+ c |
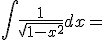 |
+ c |
Calcola gli integrali indicati e riporta i risultati negli spazi vuoti: confronta poi i tuoi risultati scaricando la traccia di soluzione
N.B. nella scittura dei risultati devi rispettare le normali convenzioni "informatiche"; niente spazi vuoti, uso di sole parentesi tonde, uso di sqrt per la radice quadrata, || per il valore assoluto, ^ per l'elevamento a potenza, / per le divisioni ...