Il concetto di integrale indefinito è estremamente semplice: non è altro che l'operatore inverso della derivata.

Si tratta infatti di trovare, data una qualunque funzione reale di variabile reale y=f(x), tutte le funzioni y=F(x) la cui derivata sia uguale a y=f(x).

Le funzioni y=F(x) si dicono anche primitive della funzione y=f(x).

Il plurale usato non è stato casuale; è evidente infatti che se una funzione y=F(x) è una primitiva della funzione y=f(x), allora anche tutte le funzioni y=F(x)+k, con k costante reale arbitraria, saranno primitive della y=f(x).

Un po' meno evidente, ma semplice da dimostrare, è invece che tutte le primitive di una stessa funzione differiscono per una costante reale.

In simboli scriveremo (utilizzando i simboli introdotti da W. G. Leibniz):

se e soltanto se

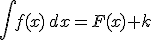
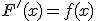N.B. Il simbolo utilizzato comprende sia il simbolo sia il dx che sembra "chiudere" la scrittura: più avanti vedremo che le due lettere dx hanno un preciso significato; per adesso limitiamoci a scrivere il simbolo completo in tutti gli integrali e pensare che dx indichi semplicemente la variabile che noi riteniamo come variabile indipendente e che non possiamo non indicare.