Introduzione
La parabola è l'insieme dei
punti del piano equidistanti da un punto detto fuoco e da una retta detta
direttrice.
Cerchiamo di trovare l'equazione di una parabola con fuoco F(0,k)
e direttrice y=-k (parabola con vertice nell'origine e asse di
simmetria coincidente con l'asse y).
Un punto del piano P(x,y) appartiene alla parabola
se 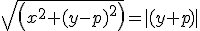
Elevando al quadrato e semplificando si ottiene 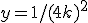 . Ponendo `
a=1/(4k) ` l'equazione della parabola diventa
. Ponendo `
a=1/(4k) ` l'equazione della parabola diventa
y=ax2
L'equazione 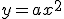 , con
, con 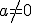 rappresenta
una parabola con:
rappresenta
una parabola con:
| vertice | V(0,0) |
|
fuoco |
F(0,1/(4a)) |
| direttrice | y=-1/(4a) |
| asse | x=0 |
Vogliamo ora determinare
l'equazione di una generica parabola P di vertice V (k,h) e con asse
di simmetria parallelo all'asse y.
La parabola P si può considerare come l'immagine di una parabola 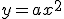 tramite una
traslazione che fa corrispondere i due vertici.
tramite una
traslazione che fa corrispondere i due vertici.
Per trovare l'equazione della
parabola P applichiamo allora alla parabola 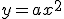 la traslazione di
vettore ` vec v (k,h) `. Otteniamo cosí l'equazione
la traslazione di
vettore ` vec v (k,h) `. Otteniamo cosí l'equazione
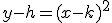
che può essere scritta dopo aver fatto qualche calcolo come
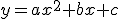 (1)
(1)
L'equazione 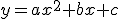 , con
, con 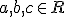 e
e
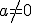 rappresenta una parabola con asse di simmetria parallelo all'asse y.
rappresenta una parabola con asse di simmetria parallelo all'asse y.
Indichiamo con 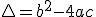 .
.
|
Il vertice è |
V(-b/(2a),- /(4a)) /(4a)) |
| Il fuoco è | F(-b/(2a),(1- )/(4a)) )/(4a)) |
| L'equazione della direttice è | y=-(1+ )/(4a) )/(4a) |
| L'equazione dell'asse è: | x=-b/(2a) |
Osserviamo che l'equazione (1)è quella di una parabola ottenuta per traslazione di vettore w (-b/(2a),
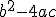 /(4a)) dalla parabola
/(4a)) dalla parabola 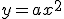 .
.Abbiamo cosí dimostrato che l'equazione
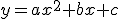 rappresenta una
parabola.
rappresenta una
parabola.
Con asse orizzontale
Se nell'equazione 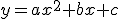 di una generica parabola P con asse di simmetria parallelo all'asse y,
si scambia x con y si ottiene l'equazione:
di una generica parabola P con asse di simmetria parallelo all'asse y,
si scambia x con y si ottiene l'equazione:
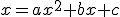
Scambiare x con y equivale ad applicare al grafico della parabola
P la simmetria rispetto alla bisettrice del primo e terzo quadrante; da
questo segue che la parabola P si trasforma in una parabola congruente,
con asse parallelo all'asse x.
Nelle relazioni scritte sopra è sufficiente scambiare le coordinate tra loro per ottenere gli elementi caratteristici della parabola
coefficienti a, b e c che compaiono nella sua equazione generale ( y = ax2 + bx + c ), risolvendo un
sistema di 3 equazioni in 3 incognite.
1. Trovare l’equazione della parabola passante per 3 punti dati.
In questo caso basta risolvere il sistema costituito dall’equazione della parabola in cui si
sostituiscono, una alla volta, le coordinate dei tre punti dati.
Esempio
Trovare l’equazione della parabola passante per A(0,1),B(1,0),C(2,3).
2. Trovare l’equazione della parabola di vertice dato e passante per un punto dato.
In questo caso una condizione è data dal passaggio per il punto dato e le altre due condizioni
dalla conoscenza delle formule per le coordinate del vertice.
Esempio
Trovare l’equazione della parabola passante per A(3,1) e per V(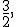
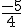 )
)
3. Trovare l’equazione della parabola di vertice e fuoco dato (oppure di vertice e direttrice dati).
In questo caso le condizioni sono date dalla conoscenza delle formule per le coordinate del
vertice e del fuoco (o del vertice e dell’equazione della direttrice).
Esempio
Trovare l’equazione della parabola avente vertice V(5,-2) e direttrice d : y = -4 .