Attività
Risolvere il seguente problema:
1) Determinare l'equazione della parabola che ha per fuoco il punto F(1;-2) e per direttrice la retta di equazione y=-3 .
Suggerimenti:
a) Ricorda che le coordinate del Fuoco sono 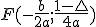
b) Ricorda che la direttrice ha equazione 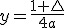
c) Imposta il sistema di tre equazioni in tre incognite
OPPURE
Ricorda la definizione di parabola e imponi che la distanza fra un punto P(x;y) e il Fuoco sia uguale alla distanza fra P e la direttrice
RISULTATO: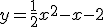
Analizziamo le posizioni delle rette di equazioni:
1) 3x-y-8=0
2) y=2x-8
3) y=-3x-5
rispetto alla parabola di equazione 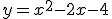
a) Dovremo considerare il sistema costituito dall'equazione della retta e dall'equazione della parabola per i tre diversi casi
1)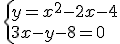 2)
2) 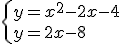 3)
3)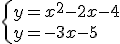
Avremo tre posizioni diverse per le tre rette rispetto alla parabola. Prova tu a verificare quali!
RETTE TANGENTI
Determiniamo le equazioni delle rette passanti per il punto P(1;-3) e tangenti alla paarbola di equazione 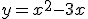
SUGGERIMENTI
a) Considera il sistema fra l'equazione del fascio di rette e la parabola:
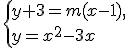
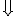
L'equazione risolvente il sistema è 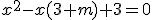 .
.
b) IMPONI LA CONDIZIONE  =0
=0
RISULTATO: m=3
N.B. Un solo valore di m perchè il punto appartiene alla parabola
Risolvere il seguente problema:
1) sia y=f(x) l'equazione della parabola, avente il vertice in (-2,-4)
e passante per l'origine degli assi; si tracci il grafico 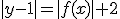 e si dica, al variare del parametro reale k, quante intersezioni ha tale grafico con la retta di equazione
e si dica, al variare del parametro reale k, quante intersezioni ha tale grafico con la retta di equazione 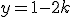
Suggerimenti:
a) l'equazione della parabola può essere trovata mediante la relazione 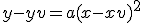 .
.
b) Quando l'hai trovata ricordati il significato del valore assoluto.
c) Ricordati anche che abbiamo lavorato sulle trasformazioni e tra le più semplici ci sono le traslazioni
d) Infine ricordati che un fascio di rette può essere di due tipi..
Buon lavoro