Dopo aver definito la densità si calcoli il peso di una sfera di legno con densità 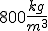sapendo che il suo volume è pari a .

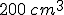E' ben noto quanto risulti importante la conoscenza della massa di un corpo per l'analisi del moto. Però, nel caso di corpi estesi ( non necessriamente fluidi ) è anche importante avere un'idea di come la massa si distribuisce nel volume, ed a tal fine si calcola il rapporto tra la massa ed il volume del corpo stesso. Tale rapporto viene detto
densità del corpo:

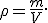
Si tratta di una grandezza scalare perchè rapporto tra due grandezze scalari.

Per risolvere l'esercizio proposto bisogna prima calcolare la massa della sfera,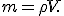
Poichè

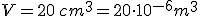, si ha

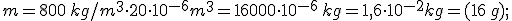
dunque il modulo del peso della sfera è:

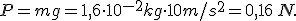
Si definisca la pressione e la sua unità di misura. Due mattoni e 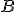sono appoggiati su un piano orizzontale. La base d'appoggio di 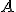è il doppio di quella di 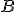ed entrambi esercitano la stessa pressione. Che relazione c'è tra i pesi dei due mattoni.

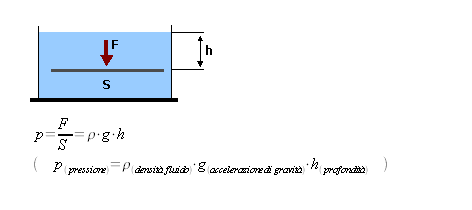
Si dice pressione il rapporto tra il modulo di una forza e la superficie su cui agisce la forza stessa. Quindi è una grandezza fisica scalare, che risulta molto utile quando la foza si distribuisce su superfici relativamente estese. A parità di intensità della forza agente la pressione è inversamente proporzionale alla superficie, ossia una stessa forza ha un effetto maggiore quando viene applicata su una superficie minore. Un esempio emblematico è dato dall'uso del chiodo, il quale riesce a forare superfici dure con una forza relativamente piccola proprio perchè la superficie su cui viene applicata la forza, la punta del chiodo, è molto piccola. Inoltre risulta utile quando si considerano masse di fluidi, proprio perchè in tal caso, in genere, il peso agisce su superfici piuttosto che in un punto specifico.
In formula, denotata con 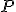la pressione, con 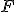il modulo della forza e con 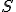la superficie su cui agisce la forza, si ha:

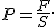
Dalla formula si ricava anche che nel S.I. la pressione viene misurata in 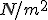, e,per definizione,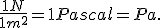

Per svolgere il problema si faccia attenzione che la pressione è la stessa, non la forza.
Dette 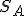ed 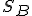la basi d'appoggio rispettivamente 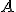di e di 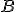, e detti 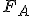ed 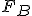i loro rispettivi pesi, dai dati del problema si ha

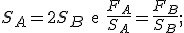
dunque

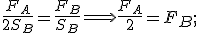
cioè il peso di 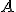è il doppio di quello di .

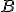Si enunci la legge di Stevino e poi si calcoli il modulo della forza agente sulla maschera di un sommozzatore a 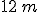di profondità in un lago, nell'ipotesi che la maschera abbia un'area di .

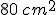Supponendo d avere un fluido ( liquido o gas ) in un contenitore, la legge di Stevino ci permette di calcolare la pressione ad una data profondità del fluido stesso. Precisamente, detta 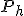la pressione a profondità 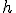, si ha:

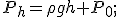
dove 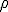denota la denssità del fluido, 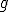è l'accelerazione di gravità, 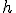la profondità e 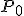la pressione atmosferica. Il fatto rilevante, deducibile dalla suddetta legge, è che la pressione non dipende dal contenitore in cui si ha il fluido, ma solo dalla profondità che si prende in considerazione.

Per calcolare la forza agente sulla maschera del sommozzatore innanzitutto, con la legge di Stevino, si calcola
la pressione a 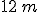di profondità:

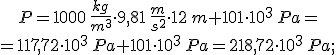
Dalla definizione di pressione, conoscendo la superficie della maschera, si può calcolare la forza 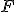agente su di essa:

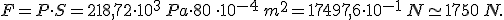
Ricordando, poi, che la forza peso è 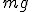, si può dire che è come se sulla maschera del sommozzatore fosse poggiata una massa di circa .

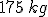Dopo aver enunciato la legge di Archimede si risolva il seguente esercizio:
una zattera di legno alta 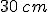e di lati 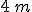e 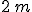, galleggia in acqua.
Qual è il volume della parte immersa? Quanto misura la parte di spigolo che emerge dall'acqua?

Il principio di Archimede ci dice che un corpo immerso in un fluido riceve una spinta ( forza ) verso l'alto pari al peso del liquido spostato, quindi se un corpo sposta un volume 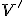di fluido, e la densità di quest'ultimo è 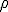, sul corpo agisce una forza verso l'alto e la sua intensità è:

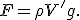
Infatti 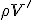è la massa del liquido spostato. Si è usato il simbolo 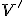per sottolineare che si utilizza il volume del liquido spostato, non quello del corpo. Per quanto riguarda il problema, intanto è necessario calcolare il volume della zattera:

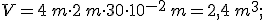
ora si potrebbe calcolare il peso della zattera: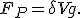

Prima di eseguire i calcoli si osservi che la zattera è in equilibrio, quindi il peso deve essere uguale in modulo e contrario in verso alla spinta di Archimede, cioè, denotando con 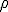la densità dell'acqua e con 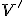il volume del liquido spostato:

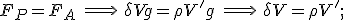
quindi il volume della parte immersa è

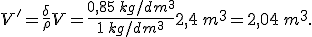
Pertanto lo spigolo immerso è

dunque la parte di spigolo emergente misura .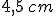

Si descriva l'esperienza di Torricelli per il calcolo della pressione atmosferica.

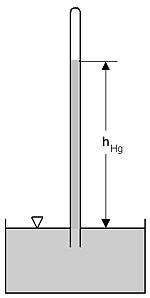
Nel 1644 Evangelista Torricelli, fisico e matematico, allievo di Galileo, riuscì ad ideare un'esperienza che gli permettesse di calcolare la pressione atmesferica. Questa suscitò, specie nelle comunita' ecclesiastiche, una certa diffidenza, soprattutto a causa di alcune indirette conseguenze (la scoperta del vuoto) difficilmente inquadrabili nella logica di alcune tradizioni religiose.

Per eseguire l'esperimento si prende un tubo lungo circa 1m e di diametro piuttosto piccolo ( qualche centimetro ) e sigillato a una estremita' , viene riempito di mercurio e posto, con l'apertura verso il basso tenuta chiusa, in una bacinella anch'essa contenente del mercurio. Aprendo l'imboccatura inferiore del tubo il mercurio comincia a defluire nella bacinella, ma raggiunta una certa altezza si ferma, il che significa che si è raggiunto l'equilibrio tra il mercurio nella bacinella e la colonna di mercurio nel tubo. Il mercurio contenuto nel tubo non e' soggetto alla pressione esterna, poichè nella parte superiore del tubo si è formato il vuoto, al contrario di quello nella vaschetta. Misurando l'altezza della colonna di mercurio rispetto alla superficie libera nella bacinella si troverà che essa è pari a 76 cm.
Al livello corrispondente alla superficie libera della vaschetta da una parte c'è la pressione atmosferisca e dall'altra la pressione della colonna di mercurio, poichè c'è l'equilibrio queste pressioni devono essere uguali. Tenendo presente la legge di Stevino per determinare la pressione della colonna di mercurio si ha:

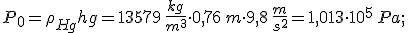
Questa è la pressione atmosferica a livello del mare. Si osservi che è stato usato il mercurio proprio per l'elevato peso specifico, usando l'acqua sarebbe stato necessario un tubo di oltre 10m!